OCTUBRE

Martes 11 de Octubre del 2016,
Pimera clase !!! =)
Indicaciones generales sobre la clase.
En la primera clase se tomaron como tema los valores como:
Respeto:
 Este se manifiesta con un saludo, atendiendo a ala persona que esta frente a nosotros.

Honestidad:
Generalmente seria realizando nuestras propias tareas y no copiando en las pruebas.

Puntualidad: 
En la clses se perimitira un retraso de 10 minutos, paso estos se debera justificar.

Compañerismo:
 El compañerismo es fundamental en algunos casos para porder realizar algunas cosas, es
copañerismos ayudar a los demas ya sea explicandoles clases o pasandoles apuntes.

Responsabilidad:
Esta se refleja en nuestras tareas, y en el estudio.

Se mensionaron los formatos que se debe llevar al momento de hacer tareas como:
*Los trabajos deben ser realizados en hojas de papel boom.
*Deberan de tener margen.
*Escribir un encabesado que conste de:
  -Nombre del establesimiento.
  -Carrera.
  -Materia.
  -Nombre del estudiante.
  -Tema.
  -Fecha esta sera la fecha de entrega del trabajo.

 Calificación.

Tareas, Trabajos, Aula Virtual, Blog    ->   (2Pts)

Pruebas   (1ra y 2da)                                ->   (4Pts)

Examen Bimestral                                   ->   (4Pts)


Viernes 14 de Octubre del 2016,
Clase #2
Muestreo y estadística descritiva:
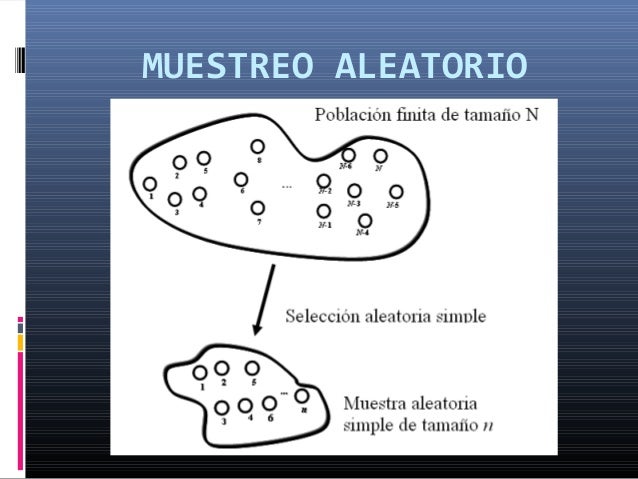
El muestreo aleatorio es uno de los mejores métodos en el proceso de la estadística.El básico es el muestreo aleatorio simple. Para comprender su concepto se hacemeja al proceso de una loteía donde todos los boletos vendidos tine las mismas probabilidades de ser escogidos como ganadores.

Población: " Representa la colección completa de elementos o resultados de la información buscada."(Navidi willia)

Muestra: Cconstituye un subconjunto de una población, que contiene elementoso resultados que realmente se observan."(Navidi willia) 

Muestra aleatoria simple:" De tamaño n es una muestra elegida por un método en el que cada colección de n elementos de la población tiene la misma probabilidad de formar la muestra, de la misma manera que en una lotería."(Navidi willia)

Para elegir este muestra aleatoria simple, se puede asignar números del 1 al N y despues seleccionar una lista de números aleatorios.

Muestra de conveniencia: "Es una muestra que no se extrae por un métodoaleatorio bien definido. "(Navidi willia)

Las muestras de conveniencia pueden diferir sistemáticamente de la población en alguna forma.Solo se usan cuando no se puede tomar una muestra aleatoria.


La muestra aleatoria simple no garantisa que refleja perfectamente a su población. Estas son siempre diferentes de sus poblaciones en algunos aspectos y considerablemente diferentes.

Variación del muestreo: "Dos muestras diferentes de la misma población también serán diferentes entre sí."(Navidi willia) 

La ventaja de una muestra aleatoria simple es que las diferencias entre muestra y población son atribuibles a la variación aleatoria. Existe una teoría matemática sobre la variación aleatoria y se pueden usar modelos matemáticos para estudiar la relación entre muestras aleatorias simples y sus poblaciones. Mientras que para una muestra que no fue seleccionada de forma aleatoria, no existe una teoría disponible y son difíciles de analizar de manera confiable.
Poblaciones tangibles: Constan de elemetos físicos reales, son simpre finitas, después de que se muestrea un elemento, el tamaño de población disminuye en 1, se podría en algunos casos regresar el elemento muestreado a la población, para muestrearlo nuevamente.

Población conceptual: "Una muestra aleatoria simple puede consistir de valores obtenidos en un proceso en condiciones experimentales idénticas. En este caso, la muestra proviene de una población que consta de todos los valores posibles que se han observado."(Navidi willia)

Los métodos estadísticos algunas veces se usan para mostrar que un conjunto de datos dado no representa necesariamente una muestra aleatoria simple. Por ejemplo, a veces las condiciones experimentales cambian gradualmente con el tiempo. Un método simple es realizar una gráfica con las observaciones en el orden en que se tomaron. Una muestra aleatoria simple no debe mostrar ningún patrón o tendencia obvia. Sin embargo, antes de tomar esa decisión, es aún importante pensar acerca del proceso que produjo estos datos, ya que en algunos casos son las características físicas del proceso de medición las que determinan si los datos constituyen una muestra aleatoria simple y puede haber cuestiones que no son evidentes en la gráfica . Se puede dar el caso para el cual una gráfica pueda parecer buena, aun cuando los datos no sean una muestra aleatoria simple.

Los métodos estadísticos pueden ayudar, especialmente cuando la muestra es grande, pero el conocimiento del mecanismo que produjo los datos es más importante.

"Los elementos en una muestra son independientes si el conocimiento de algunos de los valores de los elementos no ayuda a predecir los valores de los otros."(Navidi willia)

"Los elementos en una muestra aleatoria simple se pueden tratar como independientes en muchos casos que se encuentran en la práctica. Ocurre una excepción cuando la población es finita y la cuestra consiste de una parte importante (másde 5%) de la población."(Navidi willia)

Muestreo con reemplazo: Cuando  es posible hacer que una población se comporte como si fuera infinitamente grande, reemplazando cada elemento después de que se ha muestreado. Asi la población es exactamente la misma en cada extracción y los elementos muestreados son independientes.

Tipos de datos
 Numérico o cuantitativo:Cuando se asigna una cantidad numérica a cada elemento de una muestra.
Categóricos o cualitativos: Cuando  los elementos de la muestra son puestos en categorías.

Martes 25 de octubre del 2016,
Clase #3
Escalas de medida:

Es un instrumento con el que se asignan valores a una unidad estadística:

Tipos

Nominal:

Se asignan números a las variables, pero solo como una forma de codificación.

Ejemplos:

a)   

Hombres (0)              *Variable (Sexo)

Mujeres   (1)

b)   

 Soltero          (0)

 Casado          (1)

 Divorciado    (2)       *Variable (Estado Civil)

 Unión libre    (3)

Ordinal:

 Se asigna un orden a los calores de la variable medida.

Eejemplos:

a)  

Excelente

Bueno                       *Variable ( Atención al Cliente)

Regular

b)

Excelente

Muy Bueno

Bueno                       * Variable (Rendimiento Académico)

Regular

Insuficiente

c)

 AAA

 AA

 A                             *Variable (Calidad)

 B

 C

Escala de Intervalo:

Si se asignan valores dentro de un intervalo finito o infinito con la particularidad que existe un cero relativo.

Ejemplos:

a) Variable: Temperatura en grado Centígrado.

b)Variable: Puntuación en un examen.

 

Escala de Razón:

Si se asignan valores dentro de un intervalo finito o infinito con la particularidad que existe un "cero absoluto".

Ejemplos: 
 

a)Variable: Temperatura en grados Kelvin.

b)Variable: Estatura de una persona.

c) Variable:Tiempo de vida de un equipo.

Valores atipicos:

Se encuentra muy por encima o muy por debajo, comparado con el resto  de valores:

Ejemplo:

Como referencia la temperatura en Quito en °C:

 Datos recopilados en dos semanas:

*12  15  15  17  18  12  23

*10  12  15  12  18  20  27

*27 es un dato atípico, el mas alto de los demás. Este se puede dar por eror de medida, errores por parte del que mide.

Características de los datos.

Localización:

La posición relativa de los datos con respecto a los otros, se forman grupos de datos.

Dispersión:

La variación entre los valores medidos alrededor de la media. Se pretende medir el grado de diseminación de los datos alrededor de la media.
Ejemplo: 
En el caso de la manufactura, una alta presición esta asociada  coon una baja disperción.

Simetría:

Si los valores de la variable están distribuidos de forma similar por  ejemplo por encima y debajo de la media.

Distribucion de frecuencias.

* Sirven para resumir en una tabla numerosos datos de manera que se pongan de manifiesto las características de los datos. 

* Se utiliza para resumir datos cualitativos nominales u ordinales.

* Si los datos son cuantitativos continuos se deben previamente formar intervalos o clases.

* Se entiendo por "frecuencia absoluta" al número de veces que se repite un dato o valor en un conjunto de datos.Se simbolizará con "ni".

* la muestra es de tamaño "n".

n=n1+n2+.....nk                            

Procedimiento: 

I.-Se aplica a datos cuantitativos.

a.- Datos cuantiativos Individuales:

1.- Ordenar en forma ascendente los datos. 

2.- Colocar las frecuencias absolutas de cada dato. 

3.- Calcular la "frecuencia relativa" (fi=ni/n) 

4.- Calcular las frecuencias  acumuladas  (absolutas y relativas).

   

BIBLIOGRAFÍA:
* Navidi William, Estadistica para ingenieros y cientificos,[en linea], disponible en:https://drive.google.com/file/d/0B3NNTBVL1_YVeGk0S24zZGRxOFU/view